게임에 가장 적합한 유사 난수 발생기(PRNG)는 뭘까

프로그래밍/의문 2019. 11. 1. 18:51

일단 하드웨어 Random은 직접 Random으로 사용하는 게 아니다.
그 이유에 대해선 아래의 글을 참고.
https://stackoverflow.com/questions/39288595/why-not-just-use-random-device

c, c++에서의 rand() 함수도 고려 대상이 아니다.
일단 rand의 자체의 정밀도는 게임에 쓰기에 큰 무리 없다고는 생각하지만,
가장 문제되는 것은 랜덤 스테이트를 컨텐츠 별 지역화도 할 수 없다는 것 그리고 단일 호출로 발생되는 난수의 범위가 너무 작다는 것이다.
Visual Studio 2019 기준 rand()가 반환하는 최대 값은 32767(RAND_MAX)으로, 이것을 강제로 스케일링 해서 원하는 최대 값에 맞춰도 값은 어차피 최대 값 까지 32767 분위로 나눈 결과에 불과하기 때문에 뚜렷한 패턴이 나타나게 된다.

아래 이미지는 rand()를 1000x1000 사이즈에서 루프를 1000000만번 돌린 것을 비트맵으로 찍은 것이다.

rand를 스케일링 할때 쓴 코드는 아래와 같다.

#pragma once

#include <cstdlib>
#include <cstdint>
#include <limits>

// https://codeforces.com/blog/entry/61587
// https://en.wikipedia.org/wiki/Linear_congruential_generator
template < std::uint32_t _Max = 10000000 >
class c_rand
{
public:
	using result_type = std::uint32_t; // unsigned int 가 아니면 함수가 끝나지 않는 버그가 있다.
	static constexpr std::size_t state_size = 0;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return _Max; }
	explicit c_rand(unsigned int seed)
	{
		std::srand(seed);
	}
	inline result_type operator()()
	{
		float v = std::rand() / (float)RAND_MAX; // 스케일링 하면 값 간 정밀도가 떨어지게 됨.
		if (1.0f <= v)
		{
			return c_rand::max();
		}
		result_type ret = static_cast<result_type>(v * c_rand::max());
		return ret;
	}
};

rand를 여러번 호출하는 것으로 스케일링을 대체한다고 하면, 하면 위 이미지와 같은 뚜렷한 현상이 나오지는 않지만 그렇게 쓸 바에야 그냥 다른 알고리즘을 쓰자.

난수 발생기 중 가장 유명한 건 아마 메르센 트위스터, mt19937가 아닐까?
그냥 알고 있던 이것을 쓰려다가 mt를 만든 사람이 이후 만들었다는 well이라는 게 있다는 얘기를 듣고 간단히 찾아봤다.
mersenne twister: https://en.wikipedia.org/wiki/Mersenne_Twister
well: https://en.wikipedia.org/wiki/Well_equidistributed_long-period_linear

well은 마치 모든 면에서 mt에 비해 나은 듯 보였지만, c++ 표준에는 구현이 없다.
오픈되어있는 well의 구현 중 가장 간단한 well512의 구현을 c++ 코드로 변경했다.
그리고 c++의 uniform_distribution 같은 분포 기능들을 사용할 수 있도록 인터페이스를 맞췄다.

#pragma once

#include <cstdint>
#include <limits>
#include <random>

class well512
{
public:
	using result_type = unsigned int;
	static constexpr unsigned int state_size = 16;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	
	explicit well512(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}

	inline result_type operator()()
	{
		const result_type z0 = state[(index + 15) & 0x0fu];
		const result_type z1 = xsl(16, state[index]) ^ xsl(15, state[(index + 13) & 0x0fu]);
		const result_type z2 = xsr(11, state[(index + 9) & 0x0fu]);
		state[index] = z1 ^ z2;
		const result_type t = xslm(5, 0xda442d24u, state[index]);
		index = (index + state_size - 1) & 0x0fu;
		state[index] = xsl(2, z0) ^ xsl(18, z1) ^ (z2 << 28) ^ t;
		return state[index];
	}
private:
	// xor-shift-right
	static inline result_type xsr(unsigned int shift, result_type value) { return value ^ (value >> shift); }
	// xor-shift-left
	static inline result_type xsl(unsigned int shift, result_type value) { return value ^ (value << shift); }
	// xor-shift-left and mask
	static inline result_type xslm(unsigned int shift, result_type mask, result_type value) { return value ^ ((value << shift) & mask); }

	unsigned int index = 0;
	result_type state[state_size];
};

다음은 c++ 표준 구현체인 mt19937과의 퍼포먼스 비교이다.
vs2019에서 x64 플랫폼으로 빌드했으며, 최적화 옵션은 O2이다.
벤치마크는 google/benchmark를 이용했다.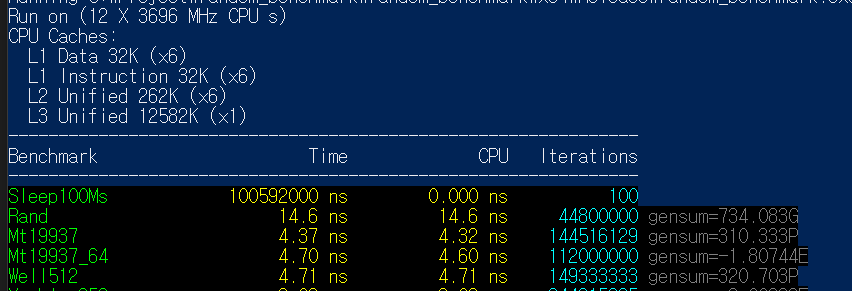

mt, well 두 알고리즘의 퍼포먼스는 비슷하게 나왔다.
다만, mt19937은 내부 상태 관리에 5000byte를 사용한다. 반면 well512는 월등하게 적은 68byte.
만약 인스턴스마다 고유 random 개체를 가져야 한다면, well은 고려해볼 옵션이라는 생각이 들었다.
다음은 mt19937과, well512를 이용해 찍은 500x500 사이즈 비트맵이다.
같은 위치에 점이 많이 찍힐수록 검게 되도록 했다.
1번: (r:204,g:204,b:204) / 2번: (r:153, g:153, b:153) / ... / 5번 이상: (r:0, g:0, b:0)

두 패턴 모두 뚜렷한 패턴이 눈에 띄진 않는다.

이후 또다른 유사 난수는 없을까 더 찾아봤다.
그리고 게임에 무슨 난수를 써야하나 고민하는 사람이 StackOverflow에 다음과 같은 글을 올린 걸 확인했다.
https://stackoverflow.com/questions/1046714/what-is-a-good-random-number-generator-for-a-game/1227137#1227137(참고로, 이 글은 2009년도에 쓰여진 글이다.)
해당 글에는 많은 얘기가 오고갔으나 질문자는 결국 MT도, WELL도 아닌 것을 선택한 모양이다.
채택이 되고 나서 9년이 지난 후 xoshiro256**을 사용한다는 글을 덧붙였다.
(xorshift: https://en.wikipedia.org/wiki/Xorshift)
너무 생소한 이름이라 그냥 그런가보다 하고 넘어갔는데, 지인에게 받은 포스트에도 xoshiro 언급이 있었다.
http://thompsonsed.co.uk/random-number-generators-for-c-performance-tested
호기심이 생겨 xoshiro와 비교적 더 최근 구현체로 보이는 xoroshiro의 구현을 c++로 옮겨서 퍼포먼스를 테스트 했다.(참고 사이트: http://prng.di.unimi.it/)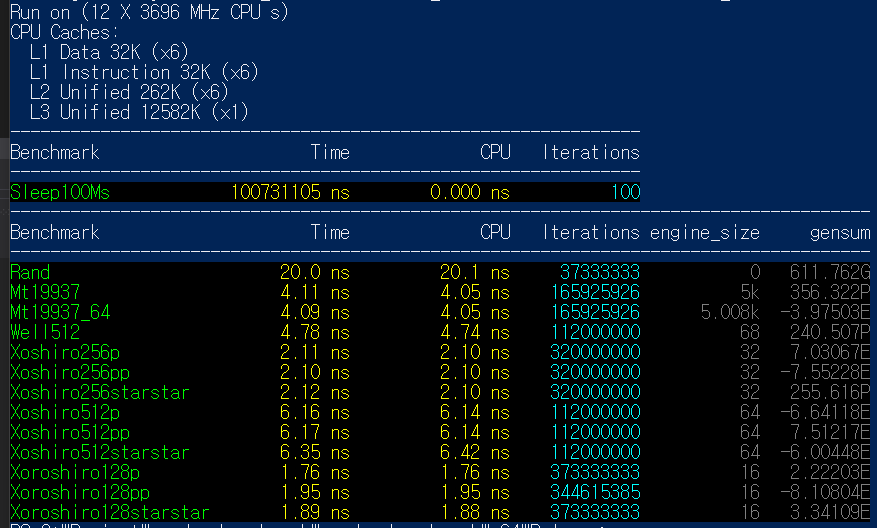

xoshiro256, xoshiro512, xoroshiro128 c++ code

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro256plus.c
/* This is xoshiro256+ 1.0, our best and fastest generator for floating-point
   numbers. We suggest to use its upper bits for floating-point
   generation, as it is slightly faster than xoshiro256++/xoshiro256**. It
   passes all tests we are aware of except for the lowest three bits,
   which might fail linearity tests (and just those), so if low linear
   complexity is not considered an issue (as it is usually the case) it
   can be used to generate 64-bit outputs, too.

   We suggest to use a sign test to extract a random Boolean value, and
   right shifts to extract subsets of bits.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoshiro256p
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 4;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro256p(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type result = state[0] + state[3];  // xoshiro256pp���� ������
		const result_type t = state[1] << 17;
		state[2] ^= state[0];
		state[3] ^= state[1];
		state[1] ^= state[2];
		state[0] ^= state[3];
		state[2] ^= t;
		state[3] = rotl(state[3], 45);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro256plusplus.c
/* This is xoshiro256++ 1.0, one of our all-purpose, rock-solid generators.
   It has excellent (sub-ns) speed, a state (256 bits) that is large
   enough for any parallel application, and it passes all tests we are
   aware of.

   For generating just floating-point numbers, xoshiro256+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoshiro256pp
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 4;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro256pp(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type result = rotl(state[0] + state[3], 23) + state[0]; // xoshiro256p���� ������
		const result_type t = state[1] << 17;
		state[2] ^= state[0];
		state[3] ^= state[1];
		state[1] ^= state[2];
		state[0] ^= state[3];
		state[2] ^= t;
		state[3] = rotl(state[3], 45);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro256starstar.c
/* This is xoshiro256** 1.0, one of our all-purpose, rock-solid
   generators. It has excellent (sub-ns) speed, a state (256 bits) that is
   large enough for any parallel application, and it passes all tests we
   are aware of.

   For generating just floating-point numbers, xoshiro256+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoshiro256starstar
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 4;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro256starstar(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type result = rotl(state[1] * 5, 7) * 9;
		const result_type t = state[1] << 17;
		state[2] ^= state[0];
		state[3] ^= state[1];
		state[1] ^= state[2];
		state[0] ^= state[3];
		state[2] ^= t;
		state[3] = rotl(state[3], 45);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro512plus.c
/* This is xoshiro512+ 1.0, our generator for floating-point numbers with
   increased state size. We suggest to use its upper bits for
   floating-point generation, as it is slightly faster than xoshiro512**.
   It passes all tests we are aware of except for the lowest three bits,
   which might fail linearity tests (and just those), so if low linear
   complexity is not considered an issue (as it is usually the case) it
   can be used to generate 64-bit outputs, too.

   We suggest to use a sign test to extract a random Boolean value, and
   right shifts to extract subsets of bits.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s.*/
class xoshiro512p
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 8;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro512p(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type result = state[0] + state[2];
		const result_type t = state[1] << 11;
		state[2] ^= state[0];
		state[5] ^= state[1];
		state[1] ^= state[2];
		state[7] ^= state[3];
		state[3] ^= state[4];
		state[4] ^= state[5];
		state[0] ^= state[6];
		state[6] ^= state[7];
		state[6] ^= t;
		state[7] = rotl(state[7], 21);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro512plusplus.c
/* This is xoshiro512++ 1.0, one of our all-purpose, rock-solid
   generators. It has excellent (about 1ns) speed, a state (512 bits) that
   is large enough for any parallel application, and it passes all tests
   we are aware of.

   For generating just floating-point numbers, xoshiro512+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoshiro512pp
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 8;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro512pp(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const uint64_t result = rotl(state[0] + state[2], 17) + state[2]; // xoshiro512p
		const result_type t = state[1] << 11;
		state[2] ^= state[0];
		state[5] ^= state[1];
		state[1] ^= state[2];
		state[7] ^= state[3];
		state[3] ^= state[4];
		state[4] ^= state[5];
		state[0] ^= state[6];
		state[6] ^= state[7];
		state[6] ^= t;
		state[7] = rotl(state[7], 21);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoshiro512starstar.c
/* This is xoshiro512** 1.0, one of our all-purpose, rock-solid generators
   with increased state size. It has excellent (about 1ns) speed, a state
   (512 bits) that is large enough for any parallel application, and it
   passes all tests we are aware of.

   For generating just floating-point numbers, xoshiro512+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoshiro512starstar
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 8;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoshiro512starstar(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const uint64_t result = rotl(state[1] * 5, 7) * 9;
		const result_type t = state[1] << 11;
		state[2] ^= state[0];
		state[5] ^= state[1];
		state[1] ^= state[2];
		state[7] ^= state[3];
		state[3] ^= state[4];
		state[4] ^= state[5];
		state[0] ^= state[6];
		state[6] ^= state[7];
		state[6] ^= t;
		state[7] = rotl(state[7], 21);
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoroshiro128plus.c
/* This is xoroshiro128+ 1.0, our best and fastest small-state generator
   for floating-point numbers. We suggest to use its upper bits for
   floating-point generation, as it is slightly faster than
   xoroshiro128**. It passes all tests we are aware of except for the four
   lower bits, which might fail linearity tests (and just those), so if
   low linear complexity is not considered an issue (as it is usually the
   case) it can be used to generate 64-bit outputs, too; moreover, this
   generator has a very mild Hamming-weight dependency making our test
   (http://prng.di.unimi.it/hwd.php) fail after 5 TB of output; we believe
   this slight bias cannot affect any application. If you are concerned,
   use xoroshiro128++, xoroshiro128** or xoshiro256+.

   We suggest to use a sign test to extract a random Boolean value, and
   right shifts to extract subsets of bits.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s.

   NOTE: the parameters (a=24, b=16, b=37) of this version give slightly
   better results in our test than the 2016 version (a=55, b=14, c=36).
*/
class xoroshiro128p
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 2;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoroshiro128p(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type s0 = state[0];
		result_type s1 = state[1];
		const result_type result = s0 + s1;
		s1 ^= s0;
		state[0] = rotl(s0, 24) ^ s1 ^ (s1 << 16); // a, b
		state[1] = rotl(s1, 37); // c
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); }
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoroshiro128plusplus.c
/* This is xoroshiro128++ 1.0, one of our all-purpose, rock-solid,
   small-state generators. It is extremely (sub-ns) fast and it passes all
   tests we are aware of, but its state space is large enough only for
   mild parallelism.

   For generating just floating-point numbers, xoroshiro128+ is even
   faster (but it has a very mild bias, see notes in the comments).

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */

class xoroshiro128pp
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 2;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoroshiro128pp(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type s0 = state[0];
		result_type s1 = state[1];
		const result_type result = rotl(s0 + s1, 17) + s0;
		s1 ^= s0;
		state[0] = rotl(s0, 49) ^ s1 ^ (s1 << 21); // a, b
		state[1] = rotl(s1, 28); // c
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); } // rotate left
	result_type state[state_size];
};

#pragma once

#include <cstdint>
#include <limits>
#include <iterator>
#include <random>

// @ref: http://prng.di.unimi.it/xoroshiro128starstar.c
/* This is xoroshiro128** 1.0, one of our all-purpose, rock-solid,
   small-state generators. It is extremely (sub-ns) fast and it passes all
   tests we are aware of, but its state space is large enough only for
   mild parallelism.

   For generating just floating-point numbers, xoroshiro128+ is even
   faster (but it has a very mild bias, see notes in the comments).

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest to seed a splitmix64 generator and use its
   output to fill s. */
class xoroshiro128starstar
{
public:
	using result_type = std::uint64_t;
	static constexpr std::size_t state_size = 2;
	static constexpr result_type min() { return 0; }
	static constexpr result_type max() { return std::numeric_limits<result_type>::max(); }
	explicit xoroshiro128starstar(std::seed_seq& seq)
	{
		seq.generate(std::begin(state), std::end(state));
	}
	inline result_type operator()()
	{
		const result_type s0 = state[0];
		result_type s1 = state[1];
		const result_type result = rotl(s0 * 5, 7) + 9;
		s1 ^= s0;
		state[0] = rotl(s0, 24) ^ s1 ^ (s1 << 16); // a, b
		state[1] = rotl(s1, 37); // c
		return result;
	}
private:
	static inline result_type rotl(const result_type x, int k) { return (x << k) | (x >> (64 - k)); } // rotate left
	result_type state[state_size];
};

다음은 각 알고리즘을 이용해 찍은 50만번 난수 생성을 하고 찍은 500x500 사이즈 비트맵이다.
같은 위치에 점이 많이 찍힐수록 검게 되도록 했다.
1번: (r:204,g:204,b:204) / 2번: (r:153, g:153, b:153) / ... / 5번 이상: (r:0, g:0, b:0)

물론 이 랜덤 비교들은 동등한 비교라고 보기 어렵다.
각 난수 발생기가 서로 다른 반복 주기를 가지며, 난수 품질도 함께 평가가 되어야 하기 때문이다.
하지만 2의 128 제곱 정도만 되어도 게임에 쓰기 이미 충분하다고 생각한다.
퍼포먼스 테스트 결과로만 보면 xoshiro, xoroshiro 시리즈가 가장 좋아 보이나 c++ 표준에는 현재 해당 알고리즘이 내장되어 않다.
조금이라도 불안감이 있다면 사용할 필요까진 없다고 판단된다.
mt의 큰 메모리 사용량도 실 사용에 있어선 문제가 되지 않을 정도이다.
어차피 랜덤 개체는 게임 내에서 컨텐츠 당 하나씩 정도이니.
난수 생성에 대한 속도 차이도 실사용에 있어선 굉장히 미미한 퍼포먼스 차이이다.
기본 LCG로 구현된 c, c++의 rand를 제외하면 어떤 걸 써도 무난해보이니 호기심은 여기서 접고 글을 마침.

결론: 현 시점에서 표준 구현이 있는 mt19937을 사용하고 추후에 다른 알고리즘들이 추가된다면 그걸 쓸 것이다.

테스트에 사용한 소스 github

zepeh92/random_bitmap (github.com)

zepeh92/random_bitmap

Contribute to zepeh92/random_bitmap development by creating an account on GitHub.

github.com

저작자표시

'프로그래밍 > 의문' 카테고리의 다른 글

왜 MTU 사이즈는 1500 bytes 인가? (0)	2020.08.05
비교문에서 상수를 왼쪽에 써야 하는 사람들의 주장 (1)	2020.06.14
c# wpf, Data Error: 40 : BindingExpression path error: ??? property not found on 'object' (0)	2019.10.09
c#, Excel Application Quit 후에도 Excel App이 종료되지 않는 현상 (0)	2019.09.24
FlatBuffer streaming 통신 (0)	2019.08.11

ABOUT ME

ZepehWAVE ZepehWAVE

'프로그래밍 > 의문' 카테고리의 다른 글

티스토리툴바

ABOUT ME

'프로그래밍 > 의문' 카테고리의 다른 글

관련글 관련글 더보기

티스토리툴바